Tornado Cash: a reference manual for developers

01 Dec, 2024

This post is written by an engineer-enthusiast (Hi, I'm Krishang 👋🏽) for fellow engineers and enthusiasts.

Please open an issue in this tornado-cash-rebuilt repository to highlight any code issues. Thanks!

This post is a follow-up to the Introduction to Zero Knowledge post. We'll be walking through the codebase of Tornado Cash in detail.

The goal is to give you a sense of the entire development cycle, and not just the Solidity smart contracts. In that spirit, we'll be covering [1] an overview of the architecture, [2] the Circom ZK circuit, [3] the smart contracts and [4] proof generation and verification on the client-side (using Javascript).

Tornado Cash was first launched in 2019. ZK tooling has grown since then, making the original repository a bit outdated. We'll walk through the tornado-cash-rebuilt repository which re-builds Tornado Cash for educational purposes using modern Solidity and ZK tooling.

Overview

The goal of Tornado Cash is to let an account (Alice) deposit 1 ether into its smart contract, and allow for another account (Bob) to withdraw Alice's deposit without creating any recognizable association between Alice and Bob.

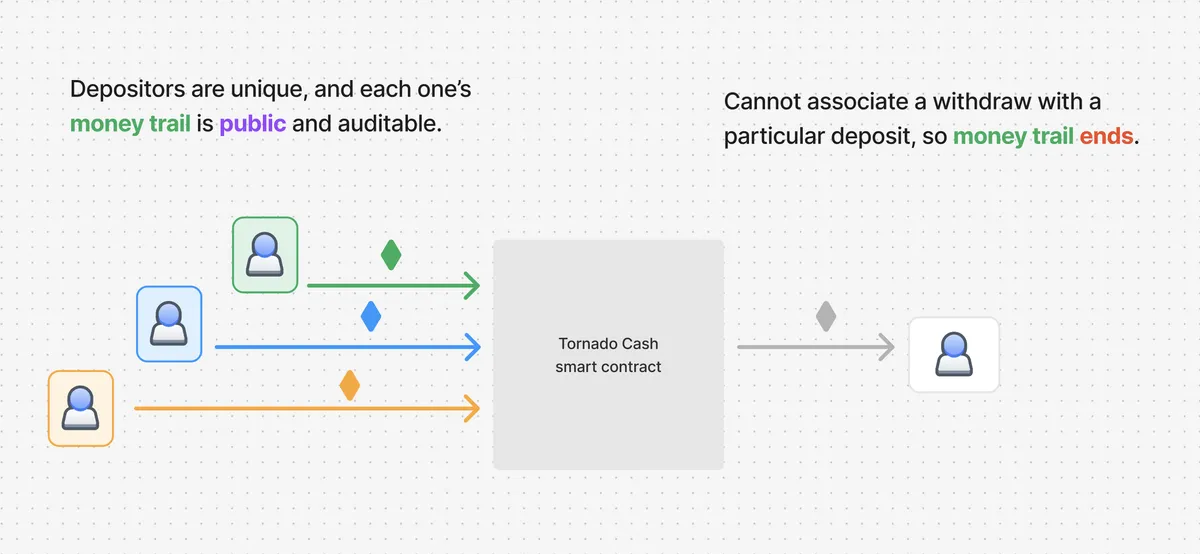
Tornado Cash achieves this by making a depositor submit a commitment along with their deposit. This commitment is the output of hashing two values together.

$C=hash(n,s)$

where $C$ is called the commitment, and $n,s$ (nullifier and secret) are private values known only to the depositor. The smart contract will now release this deposit amount to a withdrawer only if the withdrawer proves that they know $n,s$.

To prove this, if a withdrawer must reveal $n,s$ (in a direct, or indirect but recoverable way) to the smart contract, it becomes possible to create an association between a specific deposit and withdraw. That's because we can simply lookup commitment values $C$ from all deposits to the contract, and check which one satisfies $C=hash(n,s)$.

To avoid creating any association between deposits and withdrawals, Tornado Cash uses a zero knowledge proof algorithm Groth-16 to allow a withdrawer to prove their knowledge of some $n,s$ associated with a particular deposit.

Architecture

Tornado Cash consists of two smart contracts ETHTornado and Verifier, and a circuit Circuit.

1. ETHTornado: users interact with this contract's deposit and withdraw functions.

2. Verifier: its sole purpose is to verify proofs generated for the Tornado Cash circuit, and it is called during every withdrawal.

3. Circuit: it is used once in the very beginning to generate the Verifier smart contract. Later, it is used upon every withdrawal by a withdrawer who provides the private values nullifier $n$ and secret $s$ to the circuit as inputs, and receives the associated zero knowledge proof data in return as output.

To deposit 1 ether into Tornado Cash, a depositor wallet calls the deposit function on the ETHTornado smart contract, and sends along a commitment which the contract stores in a merkle tree.

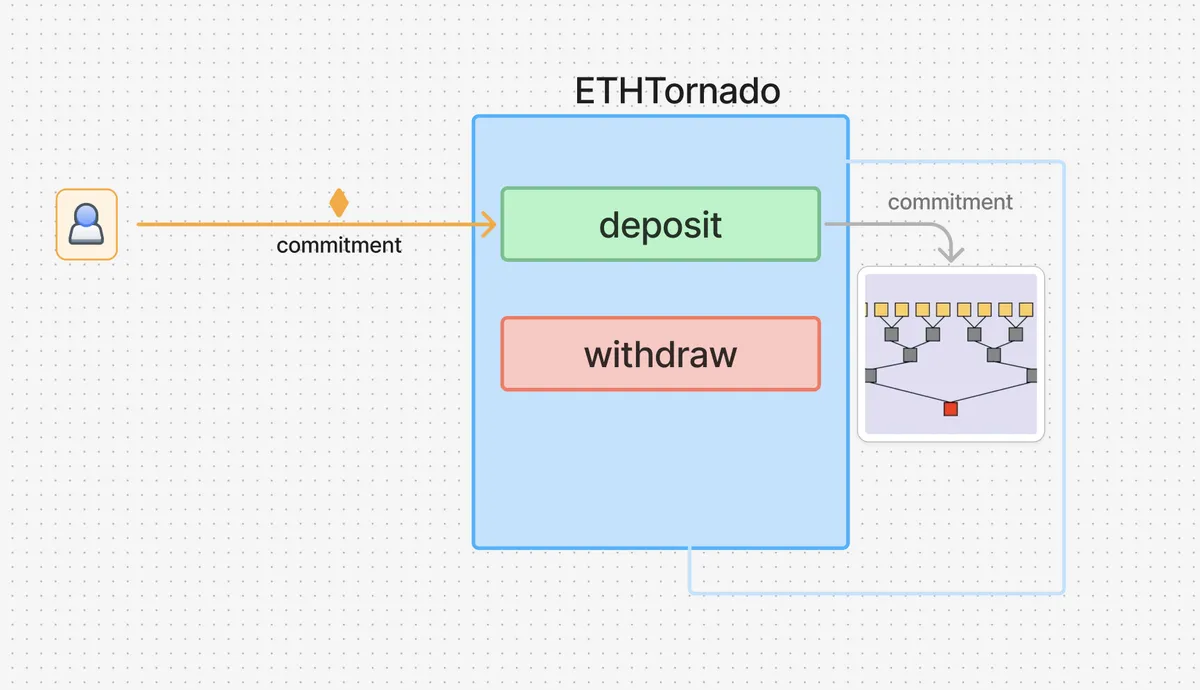
To withdraw a specific deposit, a withdrawer wallet calls the withdraw function on the ETHTornado smart contract.

To prevent creating any traceable association between the withdrawer wallet and the original depositor wallet, the contract requires the withdrawer to send a zero knowledge proof of their knowledge of the nullifier $n$ and secret $s$ associated with that specific deposit's commitment $C=hash(n,s)$.

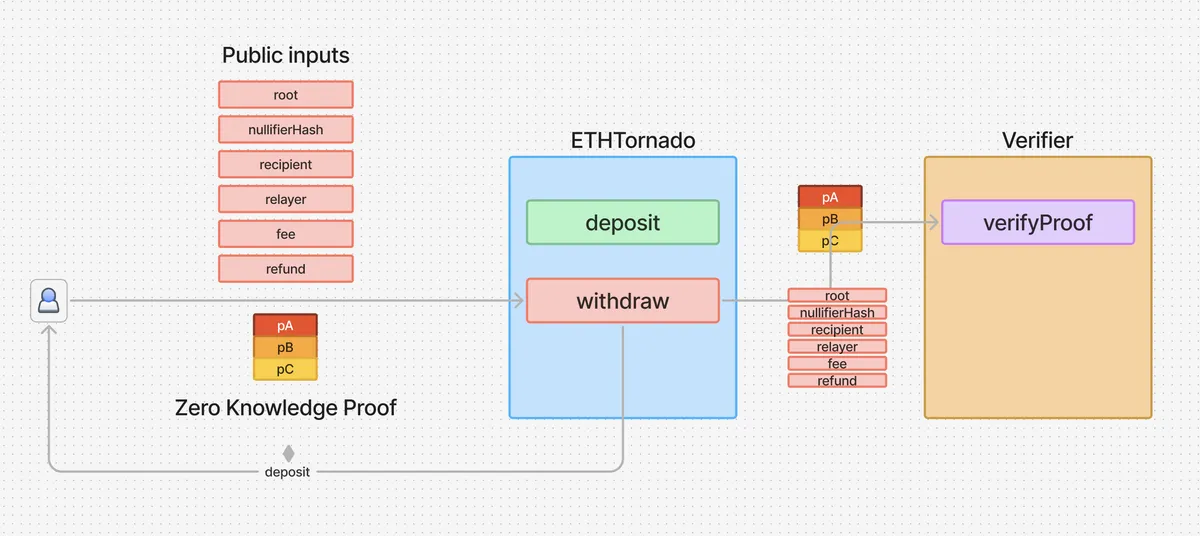
The withdrawer sends a [1] proof and [2] "public inputs" to the withdraw function. Both these values are sent to the Verifier contract, which reverts if the provided proof is faulty.

The public inputs are called so, because the withdrawer sends them plainly without any encryption or hiding.

Revealing these inputs creates important guarantees about the proof without compromising the zero knowledge nature of the proof. For example, the public input recipient is the address where the withdrawn deposit will be sent. Since the proof if generated with this specific recipient value as an input, no one can maliciously copy and use this same proof in another withdrawal transaction with a different recipient address.

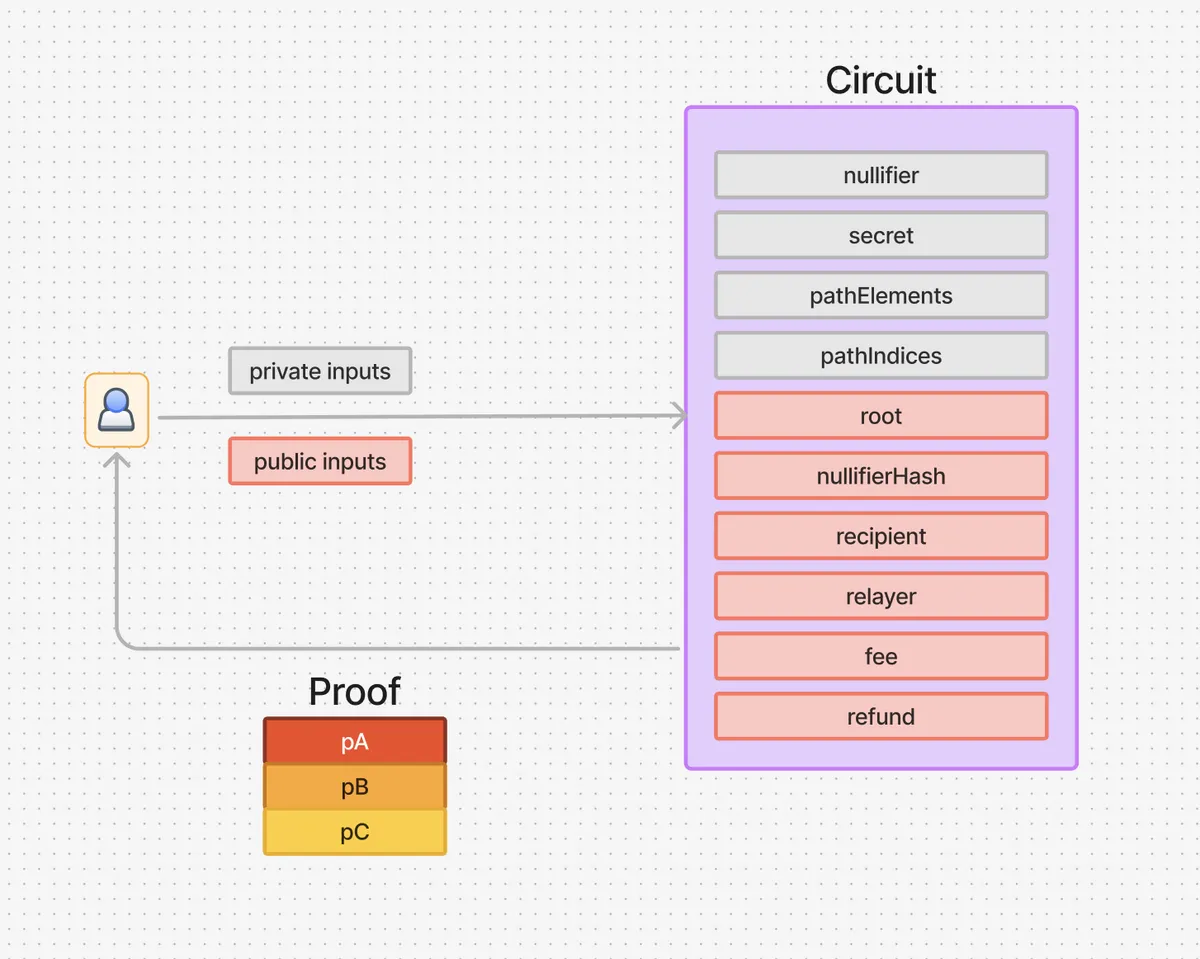
A withdrawer generates a zero knowledge proof of their knowledge of nullifier $n$ and secret $s$ by interacting with Circuit.

The circuit accepts [1] public inputs and [2] private inputs. The public inputs include a merkle root root and the private inputs include the nullifier, secret and merkle tree path elements.

The circuit hashes the nullifier and secret to compute a commitment, and using this commitment and the path elements, the circuit computes a merkle root and checks whether it is identical to the public input root.

What's a merkle tree?

This section is purely selfish. I just wanted to write a simple, clear and short explanation of merkle trees.

A merkle tree is a binary tree. It has a root which has two children, each of which have two children, ... so on.

Note how at the root level, the tree has $2^0=1$ nodes. At level-1, the tree has $2^1$ nodes, at level-2 it has $2^2$ nodes ... and at level-n the three has $2^n$ nodes.

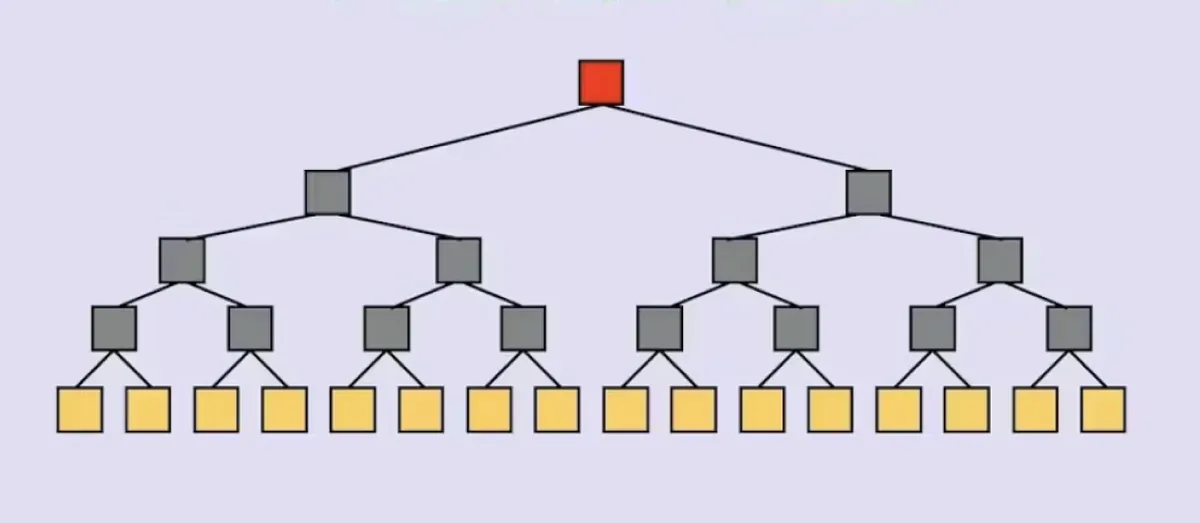
Each parent node is the hash of its two children nodes. So, $parent=hash(c_1,c_2)$. This applies to all nodes except the tree's leaves (the bottommost nodes with no children of their own).

Each leaf of the tree is a piece of "primary data". If a merkle tree has $n$ levels (not counting the root as a level), that means it can hold $2^n$ pieces of primary data. From these leaves, one can construct the entire merkle tree.

The "superpower" of a merkle tree is that if the tree holds $2^n$ leaves, it only takes $n$ pieces of data to prove that some piece of data is a leaf of the tree.

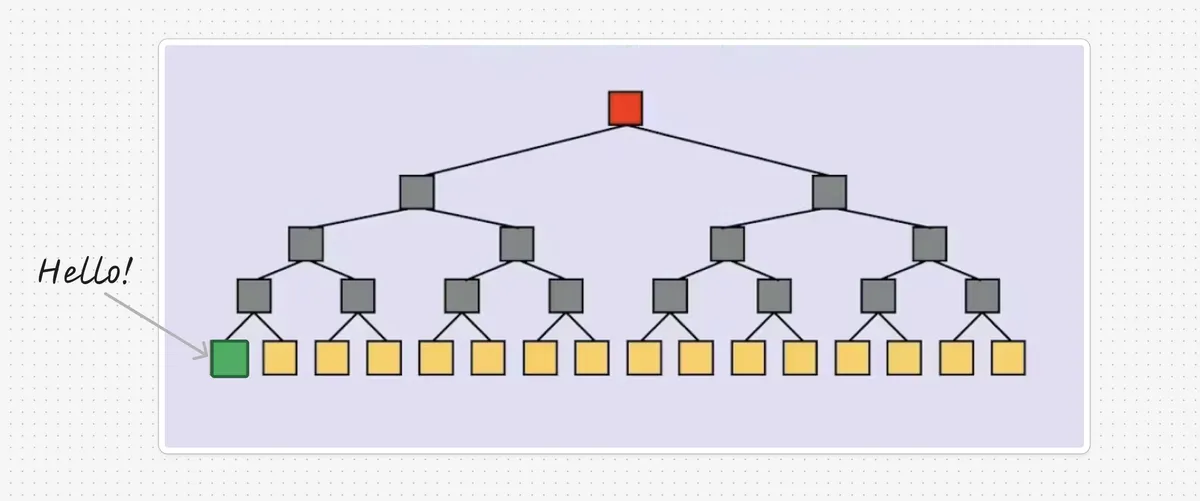
Let's say Alice has a merkle tree with $2^n$ leaves which has a root $R$. Bob has some data $d$ (the green node in the diagram) and he wants to prove to Alice that it is a leaf of the tree. If Bob sends $d$ to Alice and she naively checks $d$ against each of the leaves, that's $2^n$ operations, which is a lot.

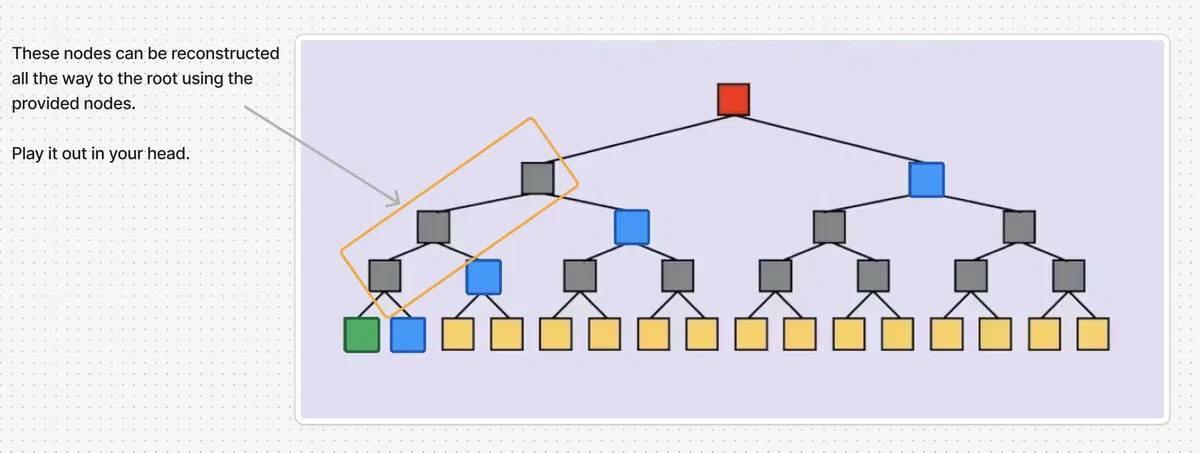
To reduce the number of operations, Bob sends $d$ along with the relevant path elements i.e. sibling, parent, grandparent, great-grandparent ... nodes of the tree (coloured blue in the diagram). Using these $n$ nodes, Alice can reconstruct a merkle tree root $R_1$ and check if it is identical to her merkle tree root $R$ to determine whether $d$ is a leaf of her merkle tree.

Code

In this section, we'll review the code behind Tornado Cash in detail. I recommend following along by cloning the tornado-cash-rebuilt repository (and give it a star while you're at it). Follow the simple README instructions to set it up.

End to end flow

Let us first look at the test_mixer_single_deposit test case to take in the end to end flow of Tornado Cash.

In the rest of the post, we'll look at each component of this test case in detail to gain a complete, low-level understanding of what's happening in this end to end flow under the hood.

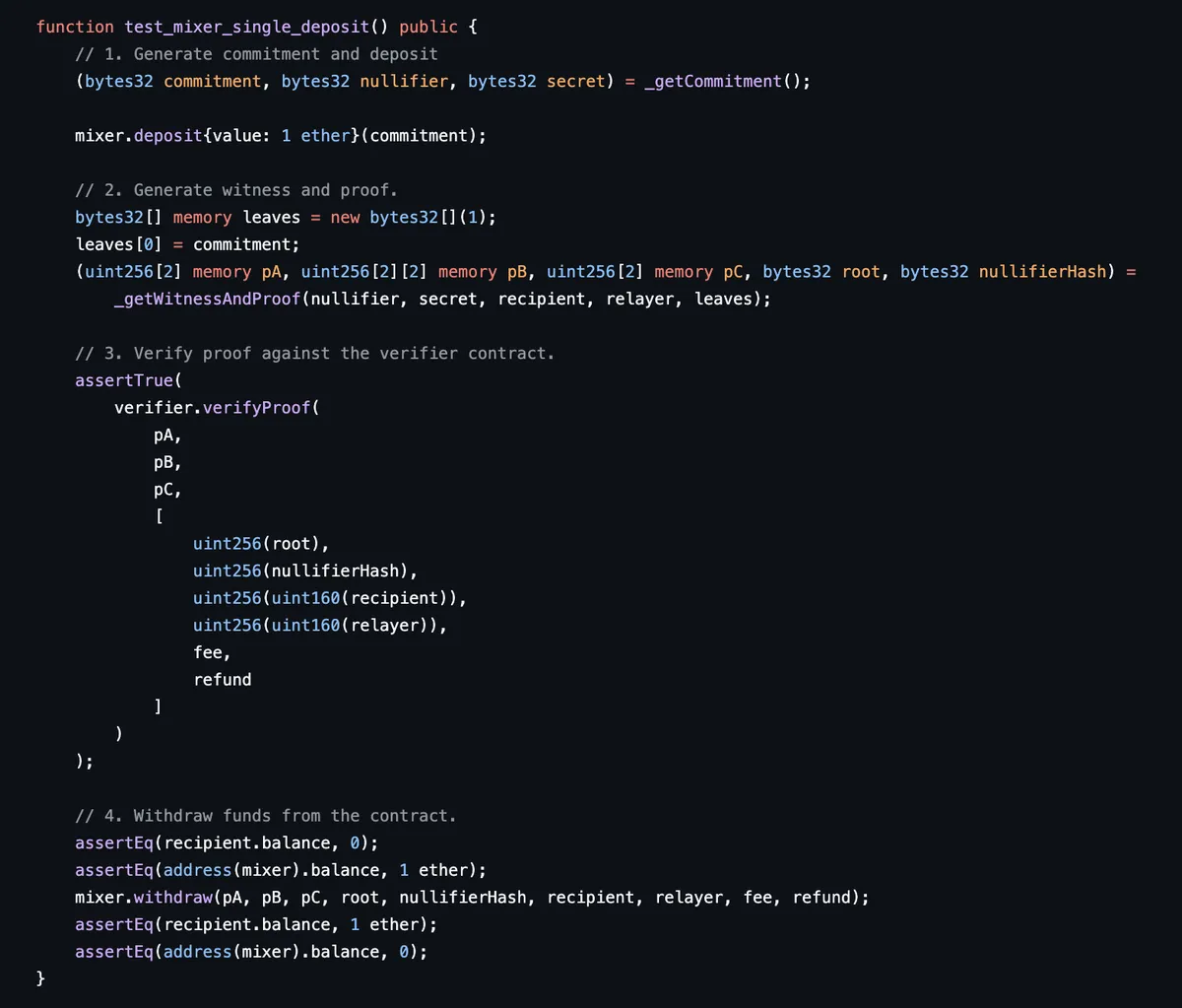
1. We generate two random bytes32 values nullifier and secret. The commitment is simply the hash of these two generated values. The depositor calls the deposit function with the commitment.

2. We generate a zero knowledge proof (of our knowledge of the nullifier and secret) using the circuit.

3. As a sanity check, we verify that our proof is a valid by directly calling the verifier contract with our proof.

4. The withdrawer calls the withdraw function with the proof and public inputs and receives the deposit.

This test itself should assure you that Tornado Cash's deposit-withdrawal flow is a typed and concrete process that we can break down step-by-step and understand completely.

Generating nullifier and secret

The _generateCommitment in step [1] uses the forge vm.ffi API to call /forge-ffi-scripts/generateCommitment.js.

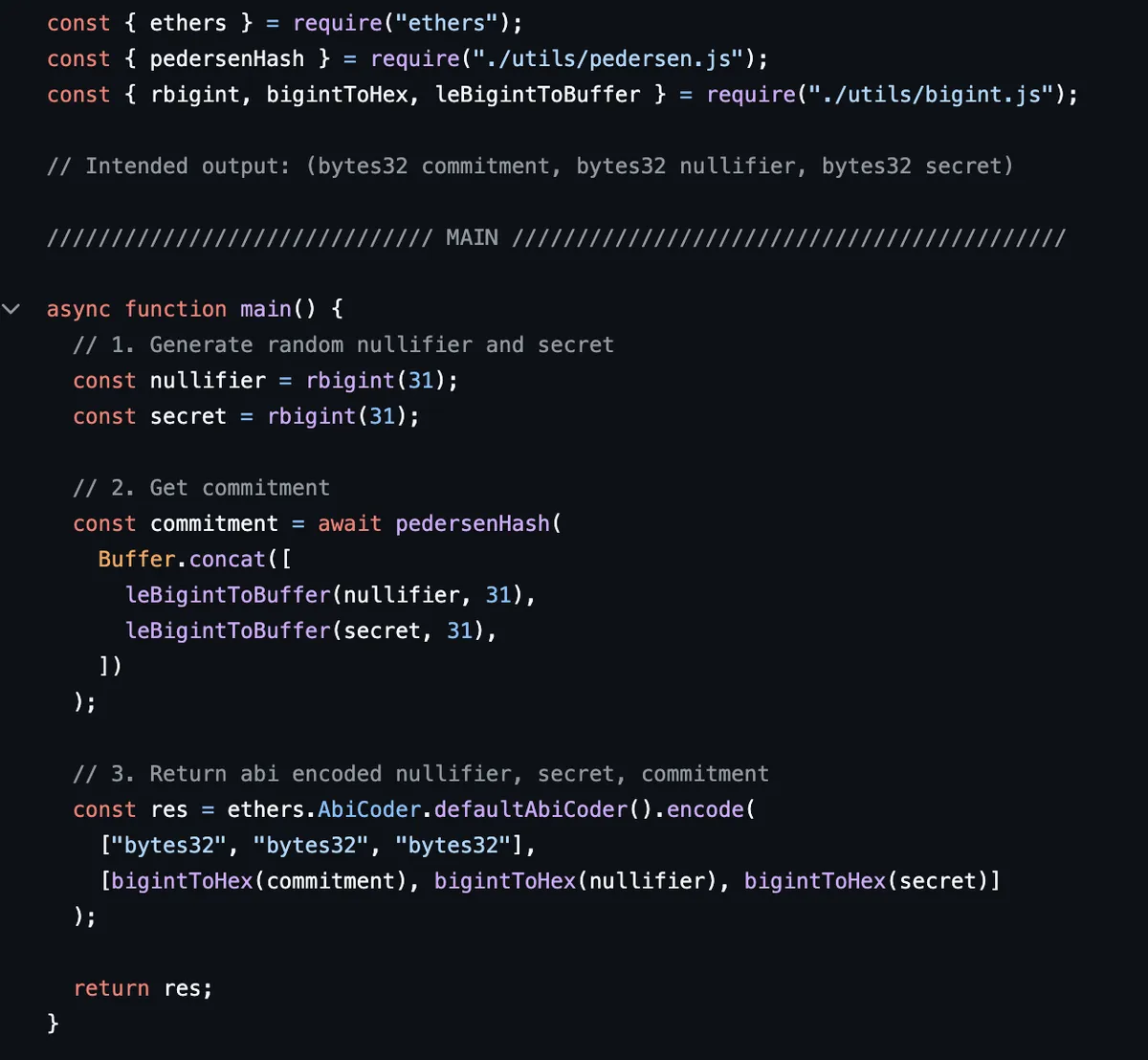
We simply generate two random numbers as our nullifier and secret, and hash them together to create our commitment.

The pedersen function is a hash function (just like keccak256 is a hash function) which is efficient in contexts of zero knowledge proofs. This means that when we use it in a circuit, it creates fewer arithmetic constraints compared to other hash functions such as the keccak hash function.

Depositing ether

The depositor calls the deposit function on the ETHTornado contract to deposit ether.

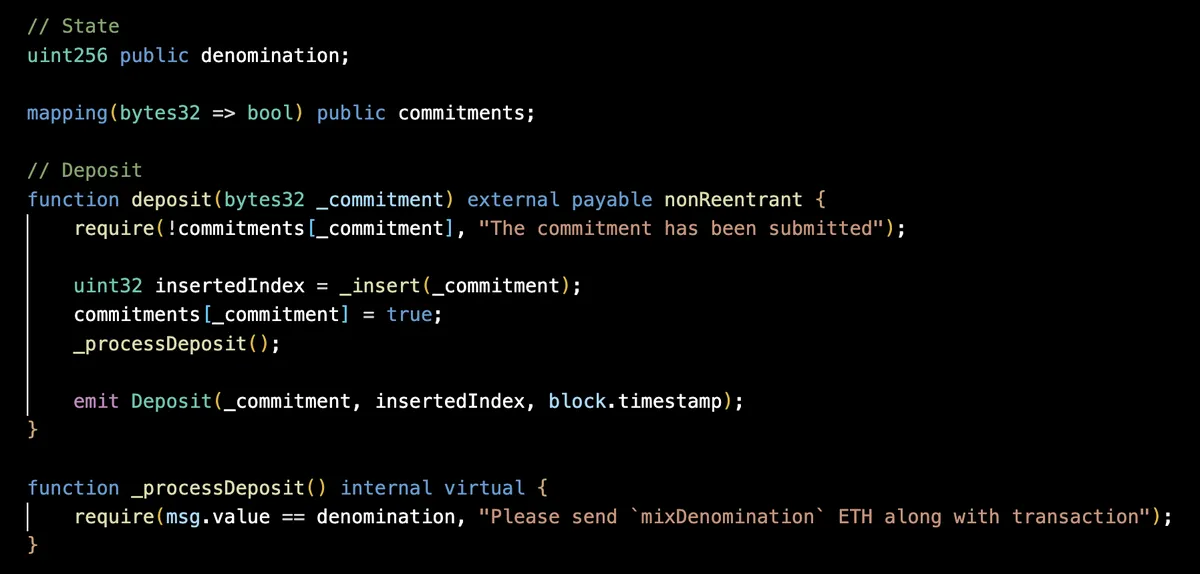
The contract marks the commitment as used, and then stores it as a leaf in its merkle tree, whose API is defined in MerkleTreeWithHistory.sol.

This is a merkle tree of fixed height and is initialized with a particular set of zeroes at each level.

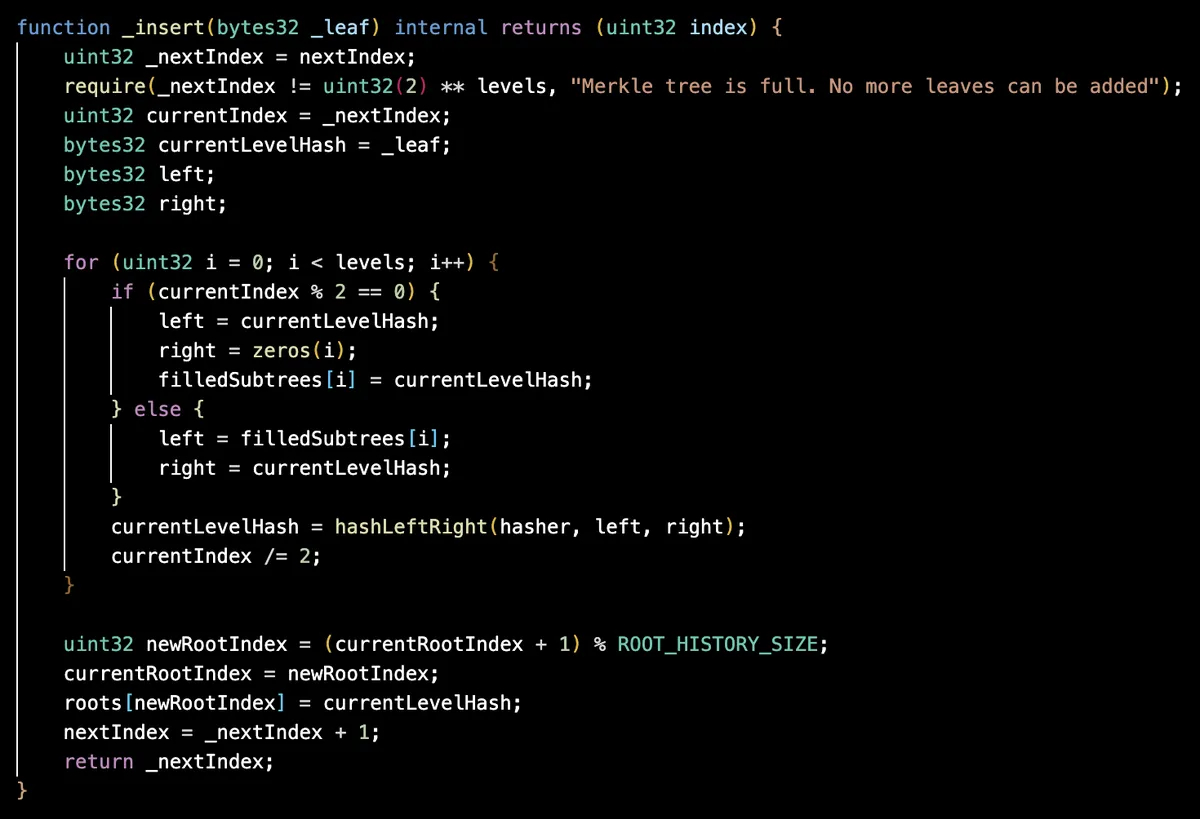
The _insert function is an algorithm for inserting leaves in the merkle tree from index $0$ to $2^n$ and updating the merkle root accordingly on each insert.

You can visualize the inserts like in the diagrams below. Each leaf of the tree is indexed. The grey nodes at every level are initialized with that level's respective zero value. The green node represent the leaf at nextIndex where we are inserting a commitment, and the blue nodes represent the nodes that are updated as a result. The yellow nodes are non-zero nodes that were updated in previous inserts.

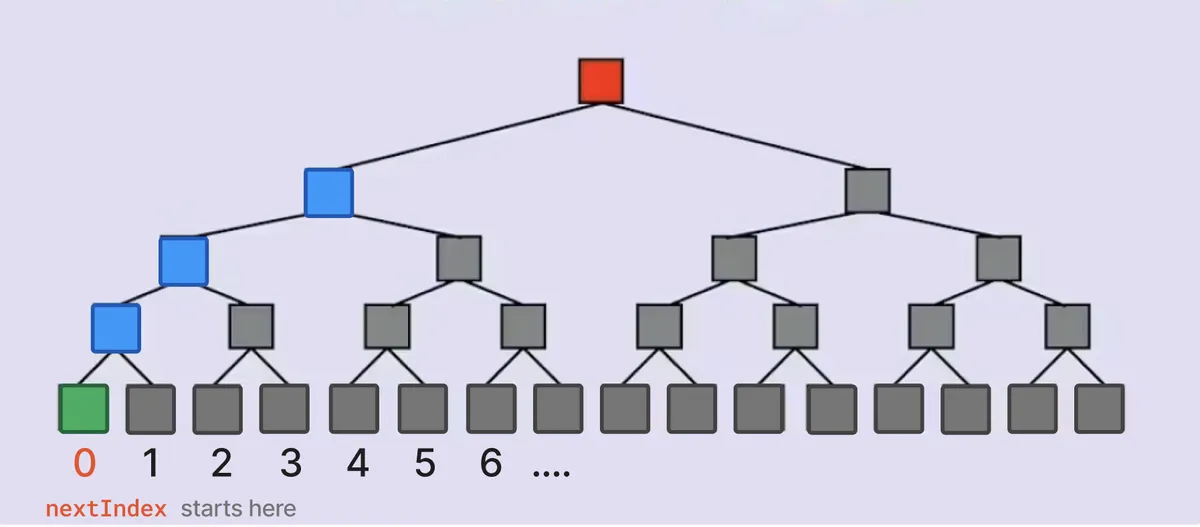
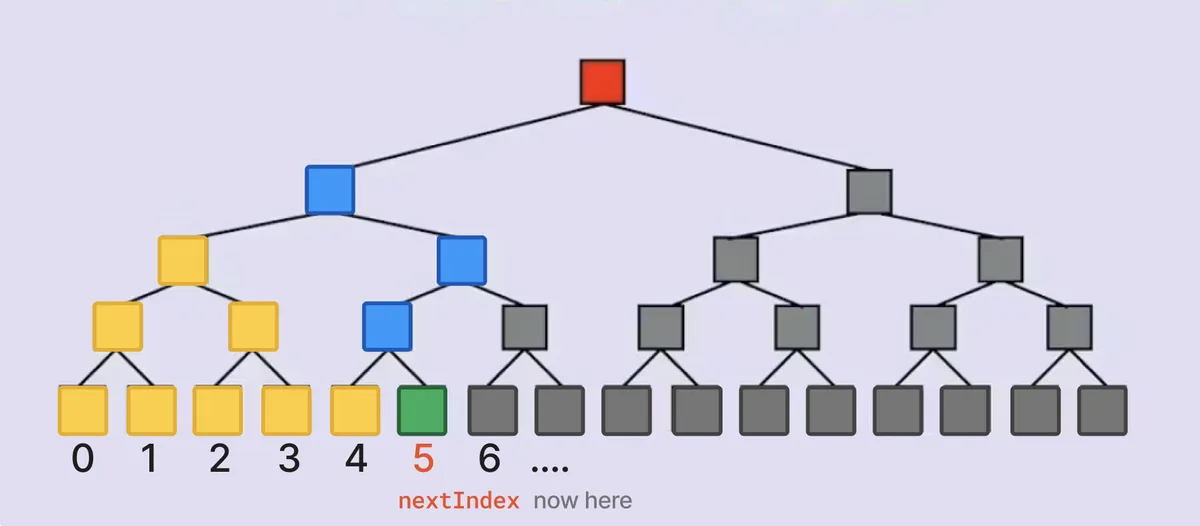
Finally, the _processDeposit call ensures that all deposits are of the same value e.g. 1 ether. That is because if someone makes a deposit of exactly 0.30024 ether and use another wallet to withdraw the same amount, the amounts of the deposit and withdraw create an association between them, which we want to avoid.

Generating proof pA, pB, pC

The _getWitnessAndProof in step [2] uses the forge vm.ffi API to call /forge-ffi-scripts/getWitness.js.

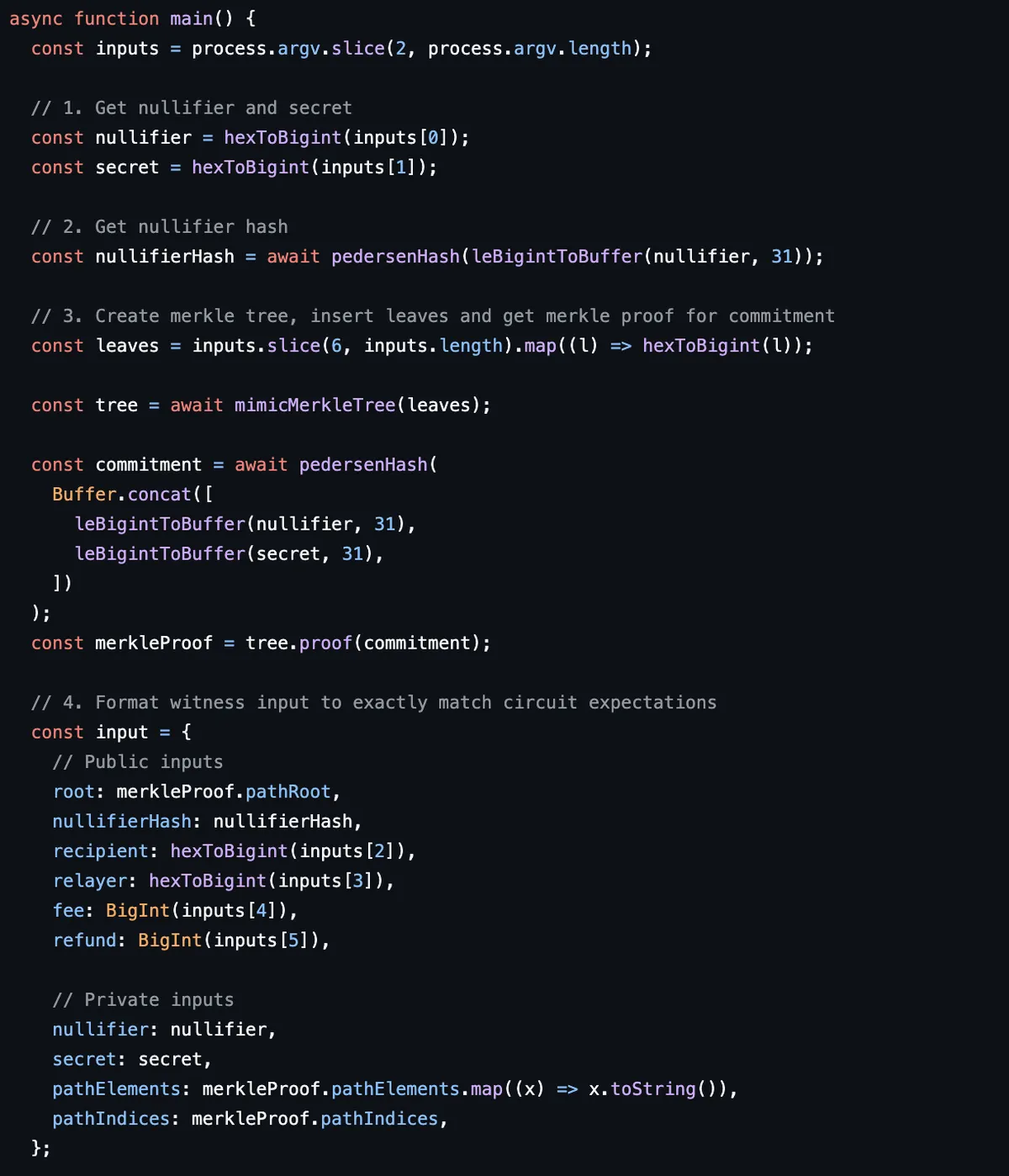
In this script, we interact with the circuit to generate a zero knowledge proof. We first assemble the inputs (private and public) to our circuit.

The mimcMerkleTree is a javascript implementation of MerkleTreeWithHistory.sol. The hash function used by the merkle tree is the MiMC hash function, which is another hash function that is efficient in the context of zero knowledge proofs.

Next, using the snarkJS library's API, we generate a proof and return in encoded in the desired format.

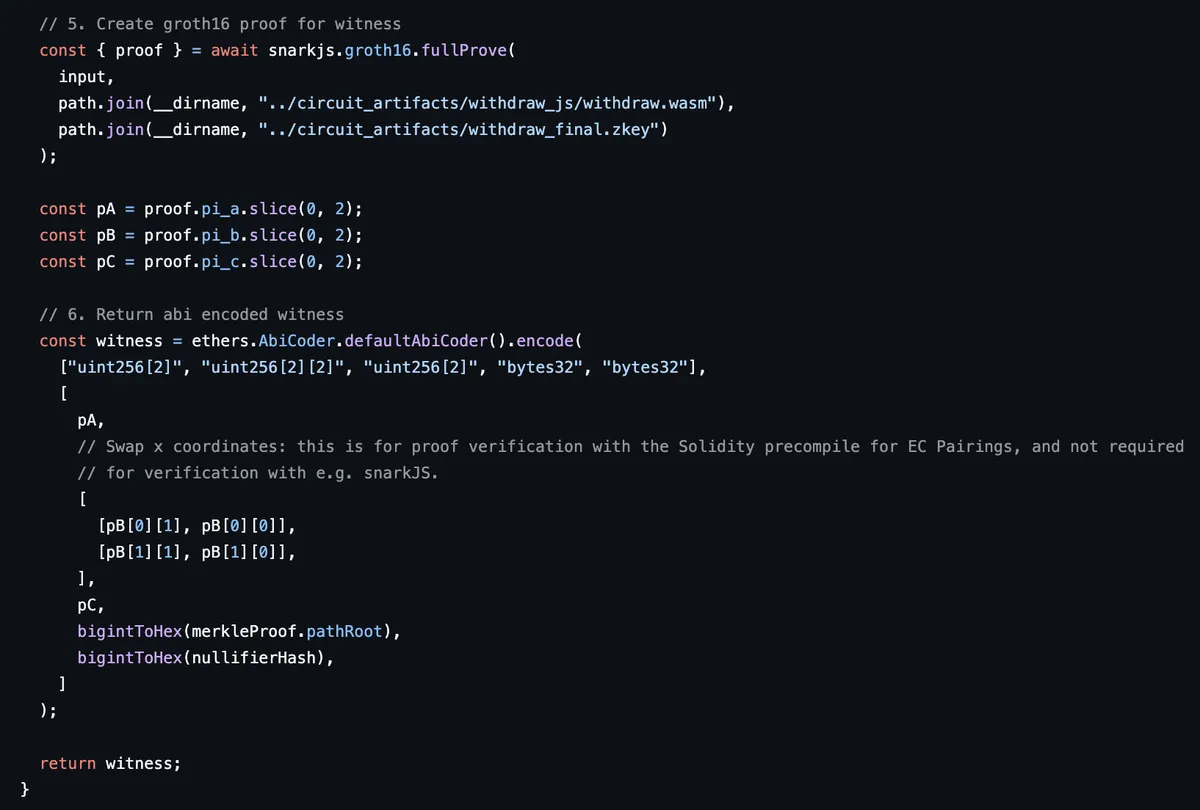
Tornado Cash circuits: withdraw.circom and merkle.circom

What does it really mean to "generate a proof" or "interact with the circuit", etc.?

Essentially, a circuit accepts inputs and performs assert statements to check that the inputs satisfy certain conditions.

Tornado Cash's circuit accepts the following inputs:

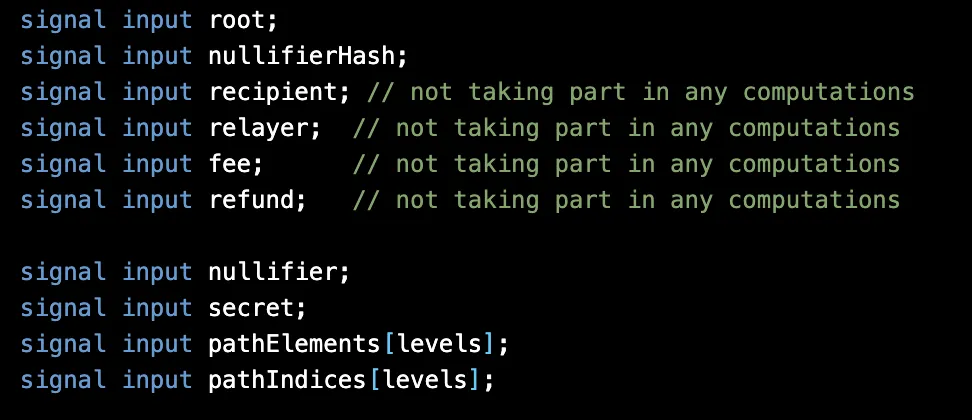
The circuit first asserts that:

hash( nullifier ) === nullifierHash

Next, the circuit does the following:

• Uses the provided nullifier and secret to compute a commitment
• Uses the commitment and the provided path elements to compute a merkle root
• Finally, it asserts that the computed root and the root provided as public input are identical.

tree(commitment, path_elements).root === root

Once you understand that this is the job of the circuit, reading the circuits (written in Circom) is not bad at all.

Finally, you'll notice the circuit use these public inputs trivially.

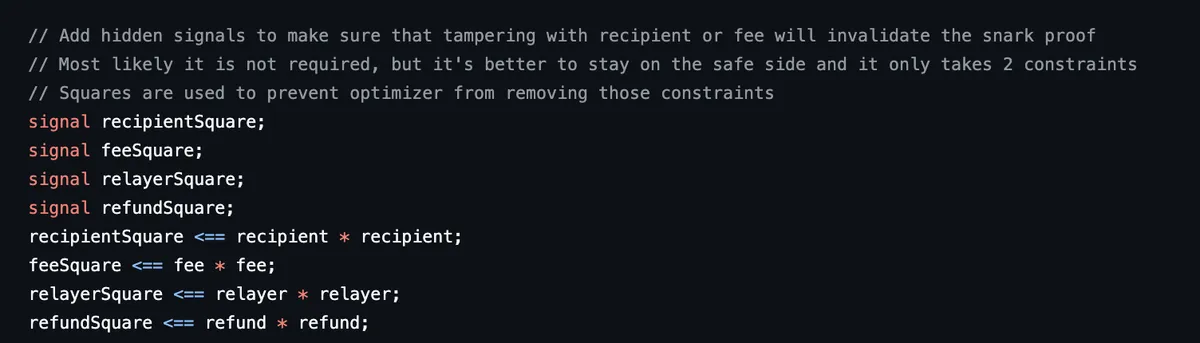
These inputs aren't involved in the assert statements mentioned above, but we do want the proof to be strictly associated with these inputs.

For example, if Bob has generated a proof with his wallet address as the recipient, we don't want a malicious third party to be able to simply re-use Bob's proof with his own wallet address as recipient. Dummy assertions such as:

(recipient * recipient) === (recipient * recipient)

make sure that the proof generated for Bob's wallet as a recipient can only be used with Bob's wallet as the recipient public input.

Verifying the proof

Once you clone the tornado-cash-rebuilt, the README instructions ask you to run make all.

This setup instruction involves:

• compiling the Tornado Cash circuits in /circuits
• providing entropy locally (in a "powers of tau ceremony")
• generating proving and verification keys (which you'll find in /circuit_artifacts)
• and finally, generating a src/Verifier.sol contract.

This contract is purpose-built to verify proofs for the specific circuit we compiled and generated proving/verification keys for.

In our test case, once we've generated our proof, we perform a sanity check by directly calling the Verifier contract's verifyProof function to check whether we've generated a valid proof.

We send our proof in the pA, pB, pC format that the Ethereum pre-compile at address 0x08 expects.

// Calling the pre-compile at 0x08 in `verifyProof`
let success := staticcall(sub(gas(), 2000), 8, _pPairing, 768, _pPairing, 0x20)

The math and algorithm behind the proof generation and verification is for another day. (Perhaps the next post? Let's see.)

Withdrawing funds

A withdrawer calls the withdraw function on the ETHTornado contract to withdraw a particular deposit.

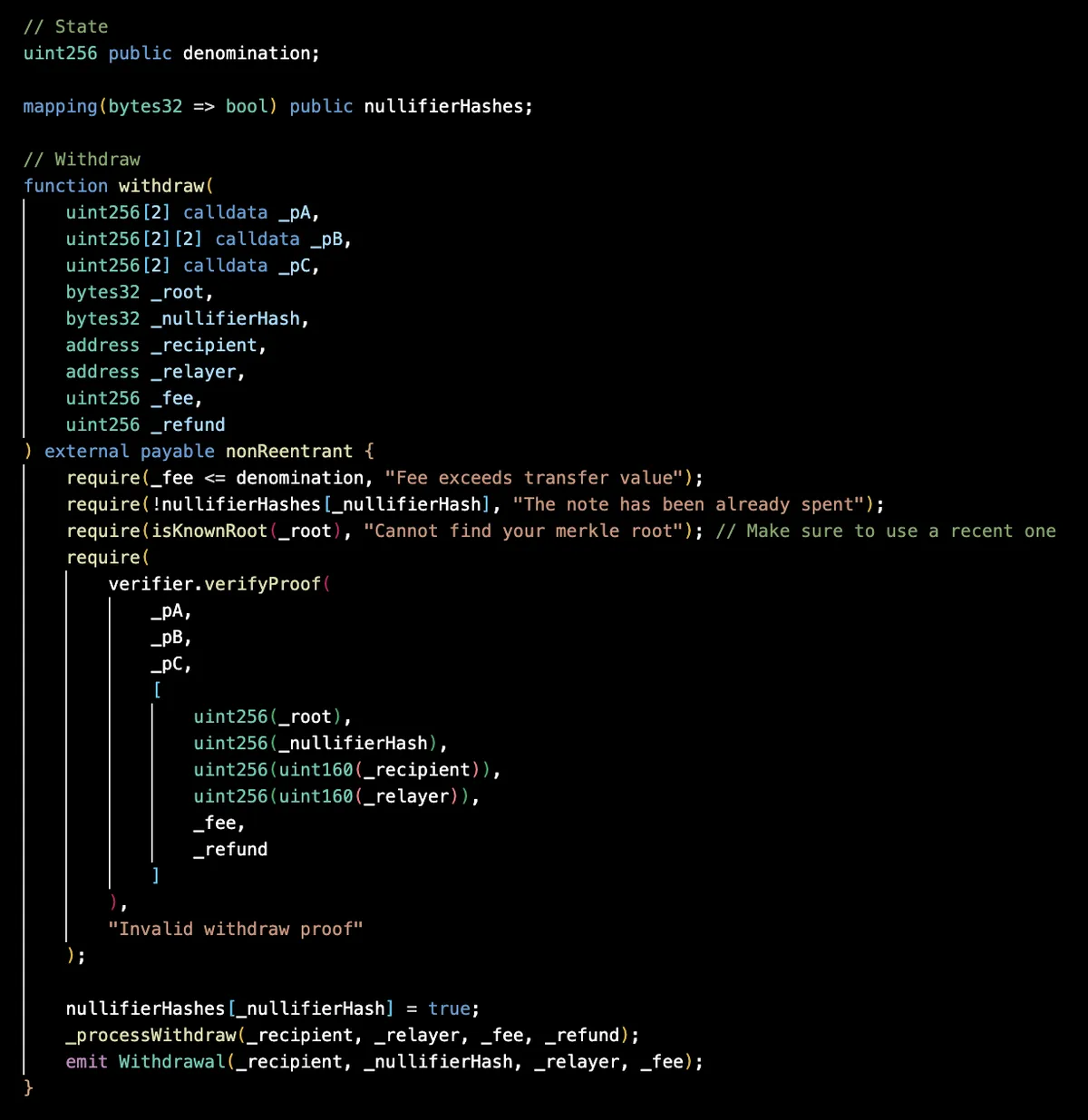
The contract ensures the proof is not being replayed by ensuring that the nullifierHash is unused. Then, it ensures that the provided public input root is the (current, or one of the past 30) root of its merkle tree via isKnownRoot.

Finally, the contract calls Verifier to verify the provided proof along with the public inputs. If the verification succeeds, the contract marks the nullifierHash as used and releases the deposit to the provided recipient address.

And that's it!

We've gone through all of the relevant code involved in the full end to end flow of using Tornado Cash -- from circuits to contracts and client side code.

This post did not cover the math behind the Groth-16 zero knowledge proof algorithm, so the how behind proof generation and verification may still remain a blackbox for you. That's alright. For example, you may not know how hash functions work under the hood but you still use them. (I have not invented this analogy, of course.)

If you have any questions or doubts about Tornado Cash stemming from this post, or any corrections you want to bring up, please open an issue in the tornado-cash-rebuilt repo, or DM me on twitter @MonkeyMeaning.