Peeling back the Zero Knowledge Onion.

26 Nov, 2024

zk-blog-header

This post is written by an engineer-enthusiast (Hi, I'm Krishang 👋🏽) for fellow engineers and enthusiasts.

It is largely based on my reading of the RareSkills ZK Book, write-ups by zksecurity, re-building tornado cash, and other such explorations.

This article introduces ZK to the point where you are armed with sufficient conceptual knowledge to explore tooling and build things without feeling like a complete LARP.

We shall peel back the ZK onion just enough to make you go "Oh, so that's what this really is", without scaring you away with math you don't really need to know (but can later choose to explore at your own discretion).

High-level Introduction

There are two parties involved in a "zero knowledge proof" -- a Prover and a Verifier.

The Prover:

knows some data $d$
which satisfies some set of constraints $C$
and proves his knowledge of that data via another piece of data $P_{d}$ .

The Verifier:

knows a set of constraints $C$
receives data $P_{d}$ from the Prover
cannot retrieve the original data $d$ from $P_{d}$
but can check $P_{d}$ to verify that the Prover knows some data $d$ that satisfies the set of constraints $C$ .

So, a "zero knowledge proof" ALGORITHM is a process that lets a Prover convince a Verifier that he knows some data that satisfies a given set of constraints, without revealing that data itself.

A "zero knowledge" PROOF is data that the Prover presents to the Verifier, which the the Verifier can check to determine whether the Prover is being honest about their knowledge of the original, un-revealed data.

What makes this process ZERO KNOWLEDGE is that the Prover never reveals the original data $d$ to anyone, in order to prove he knows $d$ .

Formal Introduction

The data $d$ is special because it satisfies a set of constraints $C$ that both the Prover and Verifier care about. The set of constraints can be thought of as a description which is true of some data, and untrue of other data.

For example, a constraint can be as simple as: $a \times b = 42$

This constraint is really a description of all pairs $(a, b)$ whose product is 42. Though this example is stupid simple and made-up, it captures a deep principle -- a set of arithmetic constraints is a description of a set of data – particularly, the set of data that satisfies those constraints.

So, phrased in another way, we can understand a zero knowledge proof as a Prover convincing a Verifier that he knows a member of a particular set, without revealing which member exactly.

A set of arithmetic constraints is a system of equations:

$z^{3} + 43 = x^{2} \cdot y$
$y - 22 = \sqrt{x} + 3 z$
... so on

A solution to a system of equations is a value assignment of all the variables that appear in the equations (e.g. $(x, y, z) = ? ?$ ). A system of equations can have none, one or many solutions.

The purpose of a zero knowledge proof is to enable a Prover to prove he knows a value assignment for the variables $(v_{1}, v_{2}, . . . v_{n})$ of a system of equations, which satisfies all equations, without revealing the particular value assignment.

In any high level application of zero knowledge proofs, such as mixers (Tornado Cash), zkVMs, private voting, etc. at the low level, there is a system of equations that encodes the high level "problem" of the application.

Practical Introduction

The "problem" of Tornado Cash is to let an account (Alice) deposit 1 ether into its smart contract, and allow for another account (Bob) to withdraw Alice's deposit without creating any recognizable association between Alice and Bob.

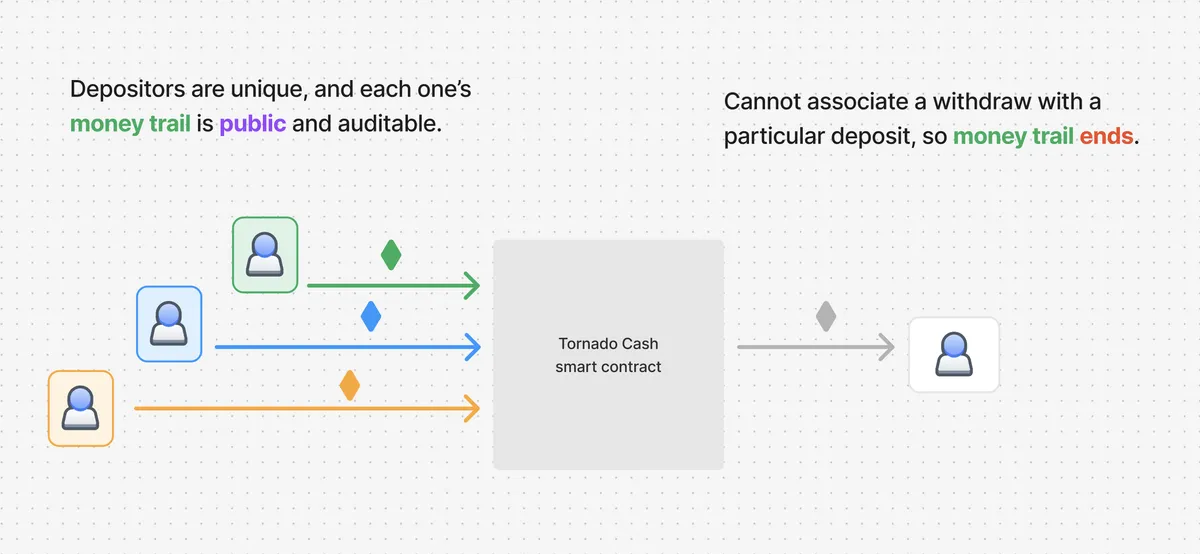
tornado-cash-diagram

Tornado Cash achieves this by making a depositor submit a commitment along with their deposit. This commitment is the output of hashing two values together.

$C = h a s h (n, s)$

where $C$ is called the commitment, and $n, s$ (nullifier and secret) are private values known only to the depositor. The smart contract will now release this deposit amount to a withdrawer only if the withdrawer proves that they know $n, s$ .

To prove this, if a withdrawer must reveal $n, s$ (in a direct, or indirect but recoverable way) to the smart contract, it becomes possible to create an association between a specific deposit and withdraw. That's because we can simply lookup commitment values $C$ from all deposits to the contract, and check which one satisfies $C = h a s h (n, s)$ .

To avoid creating any association between deposits and withdrawals, Tornado Cash uses a zero knowledge proof algorithm Groth-16 to allow a withdrawer to prove their knowledge of some $n, s$ associated with a particular deposit. Here, the smart contract acts as the Verifier and the withdrawer acts as the Prover.

Tornado Cash was first launched in 2019. ZK tooling has grown since then, making the original repository a bit outdated. We'll walk through the tornado-cash-rebuilt repository which re-builds Tornado Cash for educational purposes using modern Solidity and ZK tooling.

The /circuits directory contains code written using Circom. This code defines the set of arithmetic constraints which encode Tornado Cash's central "problem" we just learned about.

From this circuit code, we're able to generate the Verifier.sol smart contract, which acts as the Verifier of a Groth-16 proof of knowledge of some nullifier $n$ and secret $s$ such that $C = h a s h (n, s)$ for some commitment $C$ sent along with a deposit to the Tornado Cash smart contract.

Finally, the ETHTornado.t.sol test file walks through the end-to-end flow of:

Choosing a random nullifier $n$ and secret $s$ .
Generating a commitment $C = h a s h (n, s)$ and using it to make a deposit.
Generating a zero knowledge proof and making a withdrawal using it.

This post introduced Zero Knowledge to the point where you are armed with sufficient conceptual knowledge, and can now explore tooling and build things.

That said, we've just started to peel the onion, and there are many layers to go.